How to Implement a Minimalist NFT zkRollup

How to Implement a Minimalist NFT zkRollup

Zero-knowledge rollups (ZK-rollups) are layer 2 scaling solutions that increase throughput on Ethereum Mainnet by moving computation and state-storage off-chain. ZK-rollups can process thousands of transactions in a batch and then only post some minimal summary data to Mainnet. This summary data defines the changes that should be made to the Ethereum state and some cryptographic proof that those changes are correct. — Ethereum documentation

Sounds good? Why not implement our own rollup just for fun?

In this article, we will develop a minimal Zero-knowledge rollup. It is important to note that the article’s primary goal is for the reader to understand the technology, so rather than focusing on efficiency, the emphasis will be on simplicity and understandability.

The prerequisite for understanding this article is knowing the basics of ZKP technology, the Circom language, and the SnarkJS library. If these topics are all foreign to you, then it is worth reading my article on ZKP technology, as well as my article on programming with Circom and SnarkJS.

Implementing a zkRollup is not a straightforward task. Before we get started, we need to become familiar with the concept of Sparse Merkle Tree (SMT).

The Sparse Merkle Tree is a key/value storage. In this respect, it is similar to a Merkle Patricia Trie (Ethereum stores all data in such structures) but much simpler. Whereas the Merkle Patricia Tree is a complex data structure, the Sparse Merkle Tree is a simple binary tree, where each parent stores the hash of its children, with the stored values being the leaf elements, similar to a general Merkle tree. It becomes a key/value storage by having the child elements’ paths determined by the key bits. Let’s look at the following very simple Merkle tree, which is two levels deep and contains 4 values:

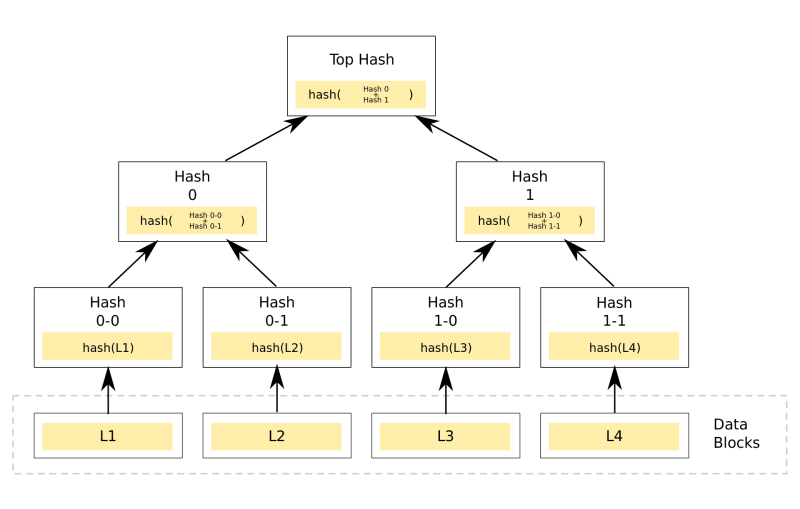
In this tree, two-bit keys can address the elements. If the key’s given bit is 0, we go left in the tree; if it’s 1, we go right. For example, if the key is 10, first we go right and then left, thus reaching the element L3. Of course, a two-bit key doesn’t make much sense in practice, and the tree’s size grows exponentially with the key’s size, hence storing such a tree requires a lot of storage capacity for large keys. So if we wanted to store, say, five numbers in the tree but the key size is 16 bits, we’d have to store 65536 values, 5 of which are meaningful and 65531 of which are 0. That is why this structure is called the Sparse Merkle Tree because we typically store far fewer values in it than its capacity. Fortunately, such a structure can be compressed quite adeptly: it is enough to go down a structure as deep as there are relevant bits.

Let’s store 3 values in the above structure. Their keys are 00, 01, 10. To store the values corresponding to keys 00 and 01, we must go to level 2, but the value corresponding to the key 10 we can store on level 1. So, we get a tree where on the left side of the root element there is a branch node with 2 leaves, whereas on the right side, there is a leaf node directly. With this “pruning” of the binary tree, we can store the elements very efficiently.

The advantage of SMT over the general Merkle tree is that it not only allows us to provide an inclusion proof but also an exclusion proof. This means that we can prove that a tree does not contain a value for the given key. Thanks to this, we can prove any operation (insert, delete, update), which will be a very important property of our rollup. Fortunately, Circomlib (and CircomlibJS) includes an SMT implementation, so we do not need to implement this ourselves.

Our rollup will store NFTs in an SMT. The NFT’s ID will be the key, with its value being the current owner’s public key. For NFTs to be transferred, the owner must produce a digitally signed transaction containing the new owner’s public key and the NFT’s identifier. The owner must prove two things: one, that they signed the transaction, and two, that they are the owner of the NFT so that their public key is stored with the NFT’s ID. If these two proofs are valid, then the ownership of the NFT will be changed to the new owner.

The sequencer collects these NFT transfer transactions, calculates the Merkle root following the transactions, and then sends the new root, list of transactions, and a zero-knowledge proof to a smart contract that proves that the sent transactions truly generate the sent root. The smart contract checks the zero-knowledge proof and if the check is successful, modifies the root.

Anyone can submit transaction batches to a smart contract if they present the corresponding zero-knowledge proofs. To do this, they need to set up the SMT which is easily accomplished since all the transactions are written on the blockchain. There is a special variation of Rollups, called Validium, where the transactions are not written on the blockchain but stored on an external repository (e.g. IPFS or Swarm). This is an even cheaper solution but we have to guarantee data availability. For example, in a DAO, we must select validators who have to sign the state root modification and only then sign the transaction after they have verified that the data is indeed available.

Here is a very simple summary graphic from Vitalik Buterin:

In a nutshell, that’s how our rollup works. Doesn’t sound too complicated, right? We’ll see from the code that the devil is in the details. Let’s take a look at the code. (Of course, all code is available on GitHub.)

For simplicity, we will pre-create the NFTs and they cannot be moved from the rollup to the blockchain (the NFTs only exist on the rollup), so it is enough to implement the NFT transfer (which itself is sufficiently complex). At the end of the article, I will explain how to further develop our rollup to enable NFTs to be moved between the blockchain and the rollup.

As a first step, let’s generate the wallet user accounts. Similar to Ethereum accounts, each Rollup account will have a private key, a public key, and an address, however, instead of ECDSA we use EDDSA for digital signing of transactions. EDDSA is a ZKP-friendly digital signature format. We’ll randomly generate the private keys and generate the addresses from the public keys with the help of Poseidon Hash (a ZKP-friendly hash algorithm). Here’s the code that generates 5 test accounts:

for (let i = 0; i < 5; i++) {
  // generate private and public eddsa keys, 
  // the public address is the poseidon hash of the public key
  const prvKey = randomBytes(32);
  const pubKey = eddsa.prv2pub(prvKey);
  accounts[i] = {
    prvKey: prvKey,
    pubKey: pubKey,
    address: trie.F.toObject(poseidon(pubKey))
  }
}

We convert the Poseidon hash to a finite field at address generation using the trie.F.toObject function.

The next step is to create the NFTs. For this, we create an SMT and fill it correctly. The key in the SMT is the NFT ID and the associated value is the address of the NFT owner. (I will write about nonce SMT later.)

// generate 5 NFTs, and set the first account as owner
for (let i = 1; i <= 5; i++) {
  await trie.insert(i, accounts[0].address)
  await nonceTrie.insert(i, 0)
}

The first task to solve is to enable users to create digitally signed transactions. A transaction consists of 3 data elements. The NFT ID of the asset to be moved, the destination address of the NFT to be sent, and a nonce. The nonce is an incrementing counter needed to make each transaction unique and only executable once. This is very similar to the solution that Ethereum uses for making transactions unique, except that Ethereum assigns the nonce to the Ethereum address, while in our case we assign it to the NFT. If we were to assign the nonce to the address, we would need a larger SMT (if the address is the key then the key size is 32-bit), so it is more practical to associate with the NFT (which needs only a 10-bit tree). Therefore the transaction is a Poseidon hash of these 3 values. This is digitally signed using EDDSA.

const createTransferRequest = (owner: Account, target: Account, 
  nftID: number, nonce: number): TransferRequest => {
  const transactionHash = poseidon([
    buffer2hex(target.address), nftID, buffer2hex(nonce)
  ])
  const signature = eddsa.signPoseidon(owner.prvKey, 
    transactionHash);
  return {
    ownerPubKey: owner.pubKey,
    targetAddress: target.address,
    nftID: nftID,
    nonce: nonce,
    signature: signature
  }
}

This transaction can be verified with the following Circom circuit:

pragma circom 2.0.0;

include "../node_modules/circomlib/circuits/eddsaposeidon.circom";
include "../node_modules/circomlib/circuits/poseidon.circom";

template VerifyTransferRequest() {

    signal input targetAddress;
    signal input nftID;
    signal input nonce;

    signal input Ax;
    signal input Ay;
    signal input S;
    signal input R8x;
    signal input R8y;

    component eddsa = EdDSAPoseidonVerifier();
    component poseidon = Poseidon(3);

    // calculate the transaction hash

    poseidon.inputs[0] <== targetAddress;
    poseidon.inputs[1] <== nftID;
    poseidon.inputs[2] <== nonce;

    // verify the signature on the transaction hash

    eddsa.enabled <== 1;
    eddsa.Ax <== Ax;
    eddsa.Ay <== Ay;
    eddsa.S <== S;
    eddsa.R8x <== R8x;
    eddsa.R8y <== R8y;
    eddsa.M <== poseidon.out;

}

The first 3 input signals (targetAddress, nftID, nonce) are the data of the transaction, while the next 5 (Ax, Ay, S, R8x, R8y) are the public key and digital signature. The circuit first calculates the poseidon hash from the data of the transaction, then verifies the digital signature and that it belongs to the given public key.

The following code snippet shows how to check the circuit using TypeScript:

const transferRequest = await createTransferRequest(accounts[0], 
  accounts[1], 1, 0)

const inputs = {
  targetAddress: buffer2hex(transferRequest.targetAddress),
  nftID: transferRequest.nftID,
  nonce: buffer2hex(transferRequest.nonce),
  Ax: eddsa.F.toObject(transferRequest.ownerPubKey[0]),
  Ay: eddsa.F.toObject(transferRequest.ownerPubKey[1]),
  R8x: eddsa.F.toObject(transferRequest.signature.R8[0]),
  R8y: eddsa.F.toObject(transferRequest.signature.R8[1]),
  S: transferRequest.signature.S,
}

const w = await verifyTransferCircuit.calculateWitness(inputs, true);
await verifyTransferCircuit.checkConstraints(w);

Every input signal of the circuit is a BigNumber. The targetAddress and the nonce are converted to hexadecimal BigNumber format using the bufer2hex function, while the Ax, Ay, R8x, and R8y signals are converted to finite field format using eddsa.F.toObject. This is necessary because, in the world of zero-knowledge proofs, all calculations are done in a finite field. For the targetAddress, the nonce, the nftID, and the S parameter, this is not necessary, since they are already mapped to a finite field.

I used the circom_tester library to check a circuit, which is a very effective solution for testing circuits since there is no need to compile the circuit for testing. The calculateWitness function calculates the witness which is then checked by checkConstraints.

The next step is to run a full transaction and generate the proof for it:

const transferNFT = async (from: Account, to: Account, nftID: number) => {
  // get the nonce for the NFT
  const nonce = BigNumber.from(
    nonceTrie.F.toObject((await nonceTrie.find(nftID)).foundValue)
  ).toNumber()

  // creating transfer request
  const transferRequest = await createTransferRequest(from, to, nftID, nonce)

  // move the NFT to the new owner
  const nft_res = await trie.update(nftID, transferRequest.targetAddress)

  // increase nonce for the NFT
  const nonce_res = await nonceTrie.update(nftID, transferRequest.nonce + 1)

  // generate and check zkp
  let nft_siblings = convertSiblings(nft_res.siblings)
  let nonce_siblings = convertSiblings(nonce_res.siblings)

  const inputs = {
    targetAddress: buffer2hex(transferRequest.targetAddress),
    nftID: transferRequest.nftID,
    nonce: buffer2hex(transferRequest.nonce),
    Ax: eddsa.F.toObject(transferRequest.ownerPubKey[0]),
    Ay: eddsa.F.toObject(transferRequest.ownerPubKey[1]),
    R8x: eddsa.F.toObject(transferRequest.signature.R8[0]),
    R8y: eddsa.F.toObject(transferRequest.signature.R8[1]),
    S: transferRequest.signature.S,
    oldRoot: trie.F.toObject(nft_res.oldRoot),
    siblings: nft_siblings,
    nonceOldRoot: trie.F.toObject(nonce_res.oldRoot),
    nonceSiblings: nonce_siblings
  }

  const w = await verifyRollupTransactionCircuit.calculateWitness(
    inputs, true
  );
  await verifyRollupTransactionCircuit.checkConstraints(w);
  await verifyRollupTransactionCircuit.assertOut(w, {
    newRoot: trie.F.toObject(nft_res.newRoot),
    nonceNewRoot: trie.F.toObject(nonce_res.newRoot)
  });

}

As a first step, we read the nonce associated with the NFT to generate the transaction. To run the transaction, we update the SMT from the owner to the new owner and increment the nonce value by one in the nonce SMT. The update function, in addition to performing the modifications, returns the siblings that are needed to prove the operation.

We check the proper execution of the circuit as usual with the checkConstraints function. If the circuit works correctly, then the two outputs must match the new roots of the SMTs.

Let’s look at the circuit that verifies the transaction:

pragma circom 2.0.0;

include "verify-transfer-req.circom";
include "../node_modules/circomlib/circuits/smt/smtprocessor.circom";
include "../node_modules/circomlib/circuits/poseidon.circom";

template RollupTransactionVerifier(nLevels) {

    signal input targetAddress;
    signal input nftID;
    signal input nonce;

    signal input Ax;
    signal input Ay;
    signal input S;
    signal input R8x;
    signal input R8y;

    signal input oldRoot;
    signal input siblings[nLevels];

    signal input nonceOldRoot;
    signal input nonceSiblings[nLevels];

    signal output newRoot;
    signal output nonceNewRoot;

    component transferRequestVerifier = VerifyTransferRequest();
    component smtVerifier = SMTProcessor(nLevels);
    component nonceVerifier = SMTProcessor(nLevels);
    component poseidon = Poseidon(2);

    // verify the transfer request

    transferRequestVerifier.targetAddress <== targetAddress;
    transferRequestVerifier.nftID <== nftID;
    transferRequestVerifier.nonce <== nonce;

    transferRequestVerifier.Ax <== Ax;
    transferRequestVerifier.Ay <== Ay;
    transferRequestVerifier.S <== S;
    transferRequestVerifier.R8x <== R8x;
    transferRequestVerifier.R8y <== R8y;

    // verify the SMT update
    // the old value of the NFT ID key has to be the poseidon hash of 
    // the signers public key, 
    // the new value is the target address 

    poseidon.inputs[0] <== Ax;
    poseidon.inputs[1] <== Ay;

    smtVerifier.fnc[0] <== 0;
    smtVerifier.fnc[1] <== 1;
    smtVerifier.oldRoot <== oldRoot;
    smtVerifier.siblings <== siblings;
    smtVerifier.oldKey <== nftID;
    smtVerifier.oldValue <== poseidon.out;
    smtVerifier.isOld0 <== 0; 
    smtVerifier.newKey <== nftID;
    smtVerifier.newValue <== targetAddress;

    // verify nonce SMT update, the new value has to be the old value + 1

    nonceVerifier.fnc[0] <== 0;
    nonceVerifier.fnc[1] <== 1;
    nonceVerifier.oldRoot <== nonceOldRoot;
    nonceVerifier.siblings <== nonceSiblings;
    nonceVerifier.oldKey <== nftID;
    nonceVerifier.oldValue <== nonce;
    nonceVerifier.isOld0 <== 0; 
    nonceVerifier.newKey <== nftID;
    nonceVerifier.newValue <== nonce + 1;

    newRoot <== smtVerifier.newRoot; 
    nonceNewRoot <== nonceVerifier.newRoot;

}

The RollupTransactionVerifier template has one parameter: the depth of the SMT. The inputs are the digitally signed transaction, the previous roots of the SMT-s, and the siblings. We have to prove that:

• The transaction is valid
• The address of the user signing the transaction is associated with the NFT moved in the SMT
• In the SMT the address associated with the NFT was modified to the new address (targetAddress)
• The nonce was increased by one in the SMT for the associated NFT.

In the first block, we verify the transaction with the VerifyTransferRequest circuit previously presented.

In the second block, we validate the SMT modification. To do this, we calculate the address of the transaction signer from the Ax and Ay parameters using a Poseidon hash. The transaction is valid if this address was originally assigned to the NFT.

We can prove SMT modification with the SMTProcessor circuit. This is a general circuit that is suitable for proving every transformation (insert, update, delete). The fnc signal determines the function of the circuit. If the fnc value is 01, we can prove an update. The transaction is valid if the old value (oldValue) linked to the nftID is the address of the signer of the transaction (the Poseidon hash of the public key) and the new value (newValue) is the tragetAddress specified in the transaction.

In the third block, we validate that the nonce in SMT has increased by one. If all conditions have been met, then the circuit output is the new root of SMT and the nonce SMT.

Now that we can validate a transaction, all that is left to do is create the final circuit that can validate a whole batch. This is what the final circuit looks like:

pragma circom 2.0.0;

include "rollup-tx.circom";
include "../node_modules/circomlib/circuits/sha256/sha256.circom";
include "../node_modules/circomlib/circuits/bitify.circom";
include "../node_modules/circomlib/circuits/poseidon.circom";

template Rollup(nLevels, nTransactions) {

    signal input oldRoot;
    signal input newRoot;

    signal input nonceOldRoot;
    signal input nonceNewRoot;

    signal input nonceList[nTransactions];
    signal input targetAddressList[nTransactions];
    signal input nftIDList[nTransactions];

    signal input AxList[nTransactions];
    signal input AyList[nTransactions];
    signal input SList[nTransactions];
    signal input R8xList[nTransactions];
    signal input R8yList[nTransactions];

    signal input siblingsList[nTransactions][nLevels];
    signal input nonceSiblingsList[nTransactions][nLevels];

    signal input transactionListHash;
    signal input oldStateHash;
    signal input newStateHash;

    // verify the transactions in the transaction list, 
    // and calculate the new roots

    var root = oldRoot;
    var nonceRoot = nonceOldRoot;
    component rollupVerifiers[nTransactions];
    for (var i = 0; i < nTransactions; i++) {
        rollupVerifiers[i] = RollupTransactionVerifier(nLevels);

        rollupVerifiers[i].targetAddress <== targetAddressList[i];
        rollupVerifiers[i].nftID <== nftIDList[i];
        rollupVerifiers[i].nonce <== nonceList[i];

        rollupVerifiers[i].Ax <== AxList[i];
        rollupVerifiers[i].Ay <== AyList[i];
        rollupVerifiers[i].S <== SList[i];
        rollupVerifiers[i].R8x <== R8xList[i];
        rollupVerifiers[i].R8y <== R8yList[i];

        rollupVerifiers[i].siblings <== siblingsList[i];
        rollupVerifiers[i].oldRoot <== root;

        rollupVerifiers[i].nonceSiblings <== nonceSiblingsList[i];
        rollupVerifiers[i].nonceOldRoot <== nonceRoot;

        root = rollupVerifiers[i].newRoot;
        nonceRoot = rollupVerifiers[i].nonceNewRoot;
    }

    // compute sha256 hash of the transaction list

    component sha = Sha256(nTransactions * 2 * 32 * 8);
    component address2bits[nTransactions];
    component nftid2bits[nTransactions];

    var c = 0;

    for(var i=0; i<nTransactions; i++) {
        address2bits[i] = Num2Bits(32 * 8);
        address2bits[i].in <== targetAddressList[i];
        for(var j=0; j<32 * 8; j++) {
            sha.in[c] <== address2bits[i].out[(32 * 8) - 1 - j];
            c++;
        }
    }

    for(var i=0; i<nTransactions; i++) {
        nftid2bits[i] = Num2Bits(32 * 8);
        nftid2bits[i].in <== nftIDList[i];
        for(var j=0; j<32 * 8; j++) {
            sha.in[c] <== nftid2bits[i].out[(32 * 8) - 1 - j];
            c++;
        }
    }

    component bits2num = Bits2Num(256);
    for(var i=0; i<256; i++) {
        bits2num.in[i] <== sha.out[255 - i];
    }

    // check the constraints

    transactionListHash === bits2num.out;
    newRoot === root;
    nonceNewRoot === nonceRoot;

    component oldStateHasher = Poseidon(2);
    oldStateHasher.inputs[0] <== oldRoot;
    oldStateHasher.inputs[1] <== nonceOldRoot;

    component newStateHasher = Poseidon(2);
    newStateHasher.inputs[0] <== newRoot;
    newStateHasher.inputs[1] <== nonceNewRoot;

    oldStateHash === oldStateHasher.out;
    newStateHash === newStateHasher.out;

}

component main {public [oldStateHash, newStateHash, transactionListHash]} = 
  Rollup(10, 8);

The main point is the first block where we invoke the RollupTransactionVerifier that we introduced earlier in an iteration. We set the root and the nonceRoot variables to the current root of the SMT and the nonce SMT respectively. Then we execute the transactions sequentially and always update the values of the root and the nonceRoot variables. After executing the transactions, we get the final roots which can be stored on the blockchain. The first version of the rollup only included this block, and the transaction data was public inputs, but it was not very efficient.

If we validate a zero-knowledge proof on-chain with a smart contract, the cost of validation depends on the number of public variables, thus the cost of validation increases with the number of transactions as well. Therefore, I modified the rollup circuit to use the sha256 hash of the transactions instead of the list of transactions. This is sufficient for validating the transactions and only 1 input instead of many. The second block thus calculates the sha256 hash of the transactions and compares it with the transactionListHash input, which is produced by the smart contract. Computing the sha256 hash in a circom circuit is a bit tricky as the order of bits is not trivial, but after a few days of research, reading, and trying out, I found the correct method for calculating the hash.

At the end of the circuit, there is still a little optimization in block 3. The circuit originally used 2 SMT roots, the NFT state root, and the nonce state root. From these I formed an oldStateHash and a newStateHash value via a Poseidon hash, so instead of 4 the number of state parameters was reduced to 2 and only 1 state root needs to be stored on the blockchain instead of 2. Therefore, the rollup finally had 3 public inputs: the oldStateHash which is the initial state, the transactionListHash which is the sha256 hash of the transaction list and the newStateHash which is the final state that will be stored on the blockchain.

This is the TypeScript code that produces the zero-knowledge proof using the above circuit, which validates a full batch:

const generateBatchTransferZKP = async (_trie: any, _nonceTrie, 
  transferRequestList: TransferRequest[]) => {
  let targetAddressList = []
  let nftIDList = []
  let nonceList = []
  let AxList = []
  let AyList = []
  let SList = []
  let R8xList = []
  let R8yList = []
  let siblingsList = []
  let nonceSiblingsList = []

  const oldRoot = _trie.F.toObject(_trie.root)
  const nonceOldRoot = _nonceTrie.F.toObject(_nonceTrie.root)

  for (const transferRequest of transferRequestList) {
    targetAddressList.push(buffer2hex(transferRequest.targetAddress))
    nftIDList.push(buffer2hex(transferRequest.nftID))
    nonceList.push(buffer2hex(transferRequest.nonce))
    AxList.push(eddsa.F.toObject(transferRequest.ownerPubKey[0]))
    AyList.push(eddsa.F.toObject(transferRequest.ownerPubKey[1]))
    SList.push(transferRequest.signature.S)
    R8xList.push(eddsa.F.toObject(transferRequest.signature.R8[0]))
    R8yList.push(eddsa.F.toObject(transferRequest.signature.R8[1]))

    const res = await _trie.update(transferRequest.nftID, 
      transferRequest.targetAddress)
    siblingsList.push(convertSiblings(res.siblings))

    const res2 = await _nonceTrie.update(transferRequest.nftID, 
      transferRequest.nonce + 1)
    nonceSiblingsList.push(convertSiblings(res2.siblings))
  }

 const newRoot = _trie.F.toObject(_trie.root)
  const nonceNewRoot = _nonceTrie.F.toObject(_nonceTrie.root)

  let transactionBuffers = []
  for (const transferRequest of transferRequestList) {
    transactionBuffers.push(numToBuffer(transferRequest.targetAddress))
  }
  for (const transferRequest of transferRequestList) {
    transactionBuffers.push(numToBuffer(transferRequest.nftID))
  }
  const hash = createHash("sha256").update(Buffer.concat(transactionBuffers))
    .digest("hex")
  const ffhash = BigNumber.from('0x' + hash).mod(FIELD_SIZE)

  const oldStateHash = poseidon([oldRoot, nonceOldRoot])
  const newStateHash = poseidon([newRoot, nonceNewRoot])

  return await snarkjs.groth16.fullProve(
    {
      targetAddressList: targetAddressList,
      nftIDList: nftIDList,
      nonceList: nonceList,
      AxList: AxList,
      AyList: AyList,
      R8xList: R8xList,
      R8yList: R8yList,
      SList: SList,
      siblingsList: siblingsList,
      nonceSiblingsList: nonceSiblingsList,
      oldRoot: oldRoot,
      nonceOldRoot: nonceOldRoot,
      newRoot: newRoot,
      nonceNewRoot: nonceNewRoot,
      transactionListHash: ffhash.toHexString(),
      oldStateHash: poseidon.F.toObject(oldStateHash),
      newStateHash: poseidon.F.toObject(newStateHash)
    },
    "./build/rollup_js/rollup.wasm",
    "./build/rollup.zkey");
}

Finally, the smart contract, which stores the state root on the blockchain, as well as validates the zero-knowledge proof:

// SPDX-License-Identifier: MIT
pragma solidity ^0.8.19;

import "./RollupVerifier.sol";
import "hardhat/console.sol";

uint256 constant FIELD_SIZE = 
  21888242871839275222246405745257275088548364400416034343698204186575808495617;

interface IVerifier {
    function verifyProof(
        uint[2] memory a,
        uint[2][2] memory b,
        uint[2] memory c,
        uint[3] memory input
    ) external pure returns (bool r);
}

contract Rollup {
    IVerifier public immutable verifier;

    event RootChanged(uint newRoot);

    uint root;

    constructor(uint _root, IVerifier _verifier) {
        root = _root;
        verifier = _verifier;
    }

    function updateState(
        uint[2] calldata _pA,
        uint[2][2] calldata _pB,
        uint[2] calldata _pC,
        uint _oldRoot,
        uint _newRoot,
        uint[16] calldata transactionList
    ) external {
        require(root == _oldRoot, "Invalid old root");

        uint256 hash = uint256(sha256(abi.encodePacked(transactionList)));
        hash = addmod(hash, 0, FIELD_SIZE);

        require(
            verifier.verifyProof(_pA, _pB, _pC, [hash, _oldRoot, _newRoot]),
            "Verification failed"
        );

        root = _newRoot;
        emit RootChanged(root);
    }

    function getRoot() public view virtual returns (uint) {
        return root;
    }

}

The rollup contract itself is relatively simple. In the constructor, it receives the initial state root and the address of the ZKP verifier contract, which can be generated from snarkjs for the circuit. The contract has a single variable named root which stores the state root and emits a RootChanged event after each batch run.

The contract has a single updateState method. The first three parameters (_pA, _pB, _pC) of the method are the zero-knowledge proof. The _oldRoot is the old state root, the _newRoot is the new state root, and the transactionList is a list of transactions. The list includes a list of NFTs that we are moving and a list of target addresses that are the new owners of the NFTs. Since our example rollup consists of 8 elements, the transactionList will be 16 elements.

First, check if the _oldRoot matches the root stored in the smart contract. Then calculate the sha256 hash of the transaction list. Since, in the case of ZKP, every calculation is done in a finite field, we need to convert the hash into a finite field, which we do with the addmod function. Then run the validation on the proof, and if everything is OK, set the new root

This is a TypeScript example code that produces the zero-knowledge proof and calls the smart contract:

trie = await newMemEmptyTrie()
nonceTrie = await newMemEmptyTrie()
let transferRequests = []
for (let i = 1; i <= BATCH_SIZE; i++) {
  await trie.insert(i, accounts[0].address)
  await nonceTrie.insert(i, 0)
  transferRequests.push(createTransferRequest(accounts[0], accounts[1], i, 0))
}

const oldRoot = trie.F.toObject(trie.root)
const nonceOldRoot = nonceTrie.F.toObject(nonceTrie.root)
const oldStateHash = poseidon.F.toObject(poseidon([oldRoot, nonceOldRoot]))

const Rollup = await ethers.getContractFactory("Rollup");
rollup = await Rollup.deploy(oldStateHash, await rollupVerifier.getAddress());

const { proof, publicSignals } = await generateBatchTransferZKP(
  trie, nonceTrie, transferRequests
)

const newRoot = trie.F.toObject(trie.root)
const nonceNewRoot = nonceTrie.F.toObject(nonceTrie.root)
const newStateHash = poseidon.F.toObject(poseidon([newRoot, nonceNewRoot]))

let transactionList: any = []
for (const transferRequest of transferRequests) {
  transactionList.push(transferRequest.targetAddress)
}
for (const transferRequest of transferRequests) {
  transactionList.push(BigNumber.from(transferRequest.nftID).toBigInt())
}

await rollup.updateState(
  [proof.pi_a[0], proof.pi_a[1]],
  [[proof.pi_b[0][1], proof.pi_b[0][0]], [proof.pi_b[1][1], proof.pi_b[1][0]]],
  [proof.pi_c[0], proof.pi_c[1]],
  publicSignals[1], publicSignals[2], transactionList
)

assert.equal(await rollup.getRoot(), newStateHash);

At the beginning of the article, we mentioned that the Rollup differs from Validium by storing the transaction list on the blockchain in the calldata. This is important because if anyone wants to submit a new batch to the smart contract, they need to build the SMTs. With Rollup, this can be easily done because every transaction is stored on the blockchain, from which the SMTs can be constructed. Let’s see the code that implements this:

trie = await newMemEmptyTrie()
 nonceTrie = await newMemEmptyTrie()

 for (let i = 1; i <= BATCH_SIZE; i++) {
   await trie.insert(i, accounts[0].address)
   await nonceTrie.insert(i, 0)
 }

 const events = await rollup.queryFilter(rollup.filters.RootChanged)
 for (const event of events) {
   const tx = await event.provider.getTransaction(event.transactionHash)
   const pubSignals = rollup.interface.parseTransaction(tx).args.at(5)
   for (let i = 0; i < BATCH_SIZE; i++) {
     const address = pubSignals[i];
     const nftID = pubSignals[BATCH_SIZE + i];
     await trie.update(nftID, address)
     const nonce = BigNumber.from(
       nonceTrie.F.toObject((await nonceTrie.find(nftID)).foundValue)
     ).toNumber()
     await nonceTrie.update(nftID, nonce + 1)
   }

   const newRoot = trie.F.toObject(trie.root)
   const nonceNewRoot = nonceTrie.F.toObject(nonceTrie.root)
   const newStateHash = poseidon.F.toObject(poseidon([newRoot, nonceNewRoot]))

   assert.equal(newStateHash, rollup.interface.parseTransaction(tx).args.at(4))

As I wrote, a smart contract emits a RootChanged event after each batch run. This is useful because it enables us to collect the transactions from which we can extract the transaction data. In the code above, we query the events with the queryFilter method. The transaction hash associated with the event is available for the full transaction, which can be extracted with the parseTransaction method for the calldata, making the transactions accessible from which the SMT can be reconstructed, which is necessary for submitting new batches.

In a nutshell, this is how the minimalist NFT rollup works. Let’s have a quick recap.

The Good

I compared a traditional NFT contract with a 64-element batch-size rollup. Moving 64 NFTs on-chain cost 2,965,696 gas, while running the 64-element batch cost only 299,575 gas. The cost of moving NFTs on rollup is thus about 10% of the on-chain solution, and we only store one root on the blockchain plus the list of transactions in the calldata (or nothing in the case of validium). This sounds pretty good. Moreover, the cost of ZKP validation does not depend on the number of transactions, so if there were 2x or 4x as many transactions in the batch, it wouldn’t be much more expensive, so even more gas could be saved, and even more space on the blockchain.

The Bad

To compile a circuit, a lot of RAM and computational capability is required. On my laptop (24G RAM, i7) the largest circuit I could compile was around 64 elements. For a larger batch-size circuit (say 256 elements), a huge amount of RAM is needed. The compile time was also around half to one hour, and the fan was really roaring. Thankfully, generating the proof for the batch was much faster, but still had to wait a few minutes. This time can probably be improved a lot by using rapidsnark for proof generation, and the technology will also probably improve a lot in the future, for example using GPU or ASICs-based proof generation.

The Ugly

As I wrote at the beginning of the article, this is a minimalistic solution, whose aim is not efficiency but rather understanding, therefore, a lot more could still be improved.

Rollups typically compress transaction data to make use of fewer calldata. Our rollup stores addresses in 32 bytes and NFT IDs in 32 bytes as well, so every transaction in the batch uses 64 bytes of calldata. That is 4096 bytes for a 64-element batch. If we were to store NFT IDs in only 4 bytes and introduce a new SMT that maps addresses to IDs, then 4 bytes would be enough to store addresses too. That would mean only 8 bytes per transaction, resulting in only 512 calldata for a 64-element batch.

The other thing we mentioned is that it is not possible to move NFTs between the rollup and the blockchain, so we have to pre-generate all NFTs and keep them on the rollup only. We did this to keep our code simple. Moving items to rollup (deposits) could be accomplished through the introduction of a new Merkle tree. If someone wants to move an NFT to the rollup, they should lock it in the smart contract and provide the rollup address which will become the owner of the NFT on the rollup. This is stored in a Merkle tree managed by the smart contract. Then, a zero-knowledge proof has to be produced, including an SMT insert proof and an inclusion proof to ensure that the same address is supplied with the NFT in the Merkle tree managed by the smart contract. If all checks out okay, then the NFT will appear on the rollup and can be moved around as previously discussed.

To withdraw an NFT onto the blockchain, an SMT delete proof has to be sent to the rollup contract, digitally signed (with EDDSA) by the current owner of the NFT, and provided an Ethereum address where the smart contract can transfer the NFT.

Summary

Zero-knowledge proof technology and zk rollups are some of the hottest fields in the blockchain world where many breakthroughs can be expected. I envision the sole duty of the blockchains of the future being the validation of zk proofs and management of state roots since every asset will exist on rollups. There will be no need to run smart contracts on the blockchain as those will run off-chain and only the state root changes will be written to the blockchain which will be validated by the accompanying zero-knowledge proof. With this solution computing and storage will be much more efficiently distributed and blockchains will be able to much higher performance. An evermore efficient yet decentralized system.

These solutions already exist in our days. An example of this is the mina protocol, where smart contracts run off-chain and the PoS validators only collect and store the transactions. Mina isn’t a blockchain since it replaces it with recursive proofs. Each block contains a proof of the validity of the previous block. Thanks to this, the “blockchain” of mina is only 22KB in size.

The future is very exciting. It is therefore worthwhile to get acquainted with zero-knowledge proof technology, as it is becoming an increasingly integral part of the blockchain world.

Originally published here: https://hackernoon.com/how-to-implement-a-minimalist-nft-zkrollup-with-circom-and-snarkjs